Átomo hidrogenoide en coordenadas parabólicas
En este artículo vamos a tratar de obtener, usando la teoría cuántica, unas ecuaciones que nos permitan estudiar los átomos hidrogenoides, aunque la resolución la veremos en otro post donde usaremos Python y algunas librerías interesantes para este tipo de problemas. Partiremos de un cambio a coordenadas parabólicas y después usando un tratamiento semiclásico llegaremos al resultado buscado.
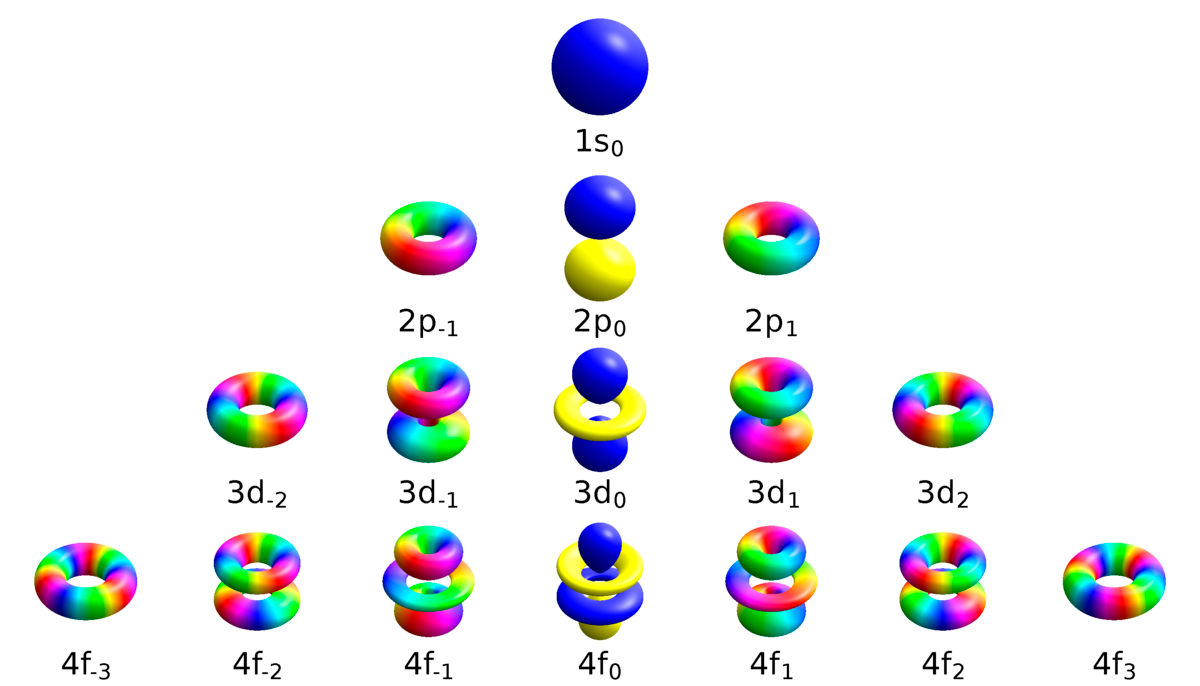
Introducción
Sea el cambio entre coordenadas cartesianas y parabólicas:
\[\begin{alignat*}{2} & \begin{cases} x=\sqrt{\xi\eta}\cos(\phi),& 0\leq \xi\\ y=\sqrt{\xi\eta}\sin(\phi),& \eta < \infty \ ;\\ z=\frac{1}{2}(\xi - \eta) \end{cases} && \begin{cases} \xi=r+z,& \\ \eta=r-z,& \\ \phi=\arctan(\frac{y}{x}) \end{cases} \end{alignat*}\] \[\begin{equation*} r=\sqrt{x^2+y^2+z^2}=\frac{1}{2}(\eta+\xi) \end{equation*}\]Hablando de un modo poco riguroso, un átomo hidrogenoide consiste en un electrón orbitando el núcleo que está formado por uno o más protones (un protón en el caso del hidrógeno). Así, podemos enfocar este problema como el de los dos cuerpos.
Sea $m_1$ la masa del electrón y $m_2$ la del núcleo, la energía del sistema es:
\[\begin{equation*} E=\frac{p_1^2}{2m_1}+\frac{p_2^2}{2m_2}+E_{potencial} \end{equation*}\]donde $p_1$ y $p_2$ son los módulos del momento de cada cuerpo $\vec{p}_i=\vec{v}_i\cdot m_i$.
El operador momento en mecánica cuántica se define como:
donde $\vec{\nabla}=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)$.
Es trivial ver que
\[\begin{equation*} \left[\hat{p}_1,\hat{p}_2\right]=-\hbar^2\left[\vec{\nabla}_1,\vec{\nabla}_2\right]=0, \end{equation*}\]por tanto podemos medir sus observables asociados simultáneamente lo que nos permite simplificar la expresión de la energía.
Análisis clásico
La energía cinética del sistema en términos del módulo de la velocidad:
\[\begin{equation*} T=\frac{1}{2}m_1v_1^2+\frac{1}{2}m_1v_2^2 \end{equation*}\]El objetivo es expresar $T$ en función de un término que dependa del centro de masas más otro que dependa de las coordenadas relativas. Esto nos interesa ya que la masa del núcleo es mayúscula en comparación a la del electrón.
\[\begin{equation*} T=T_{CM}+T_{rel} \end{equation*}\]Basándonos en un análisis esquemático en dos dimensiones, en mecánica clásica se define:
\[\begin{equation} \begin{cases} \vec{r}_{CM}\equiv\frac{m_1\vec{r}_1+m_2\vec{r}_2}{m_1+m_2}& \\ \vec{r}\equiv\vec{r}_1-\vec{r}_2 \end{cases} \label{eq:cm} \end{equation}\]Queremos expresar $\vec r_{1}$ y $\vec r_{2}$ en función de $\vec{r}_{CM}$ y $\vec{r}$. Resolvemos el sistema planteado por el cambio propuesto en \eqref{eq:cm} obteniendo:
\[\begin{equation*} \begin{cases} \vec{r}_1=\vec{r}_{CM}+\frac{m_2}{M}\vec{r}& \\ \vec{r}_2=\vec{r}_{CM}-\frac{m_1}{M}\vec{r} \end{cases} \end{equation*}\]donde $M=m_1+m_2$ es la masa total del sistema.
Ahora podemos calcular la energía $T$ como sigue:
Donde hemos usado $\dot{\vec r}_{CM}=\vec{v}_{CM}$.
Análogamente para $\vec{v}_2$
\[\begin{align*} v_2^2&=v_{CM}^2+\frac{m_1^2}{M^2}|\dot{\vec{r}}|^2-2\frac{m_1}{M}\dot{\vec{r}}_{CM}\cdot\dot{\vec{r}} \end{align*}\]Entonces
\[\require{cancel}\begin{align*} T&=\frac{1}{2}m_1\left(v_{CM}^2+\frac{m_2^2}{M^2}|\dot{\vec{r}}|^2+\cancel{2\frac{m_2}{M}\dot{\vec{r}}_{CM}\cdot\dot{\vec{r}}}\right)+\frac{1}{2}m_2\left(v_{CM}^2+\frac{m_1^2}{M^2}|\dot{\vec{r}}|^2-\cancel{2\frac{m_1}{M}\dot{\vec{r}}_{CM}\cdot\dot{\vec{r}}}\right)\:=\\ &=\frac{1}{2}M\cdot v_{CM}^2+\frac{1}{2}\frac{|\dot{\vec{r}}|^2}{M^2}\underbrace{m_1m_2^2+m_2m_1^2}_{m_1m_2(\underbrace{m_1+m_2}_{M})}=\underbrace{\frac{1}{2}M\cdot v_{CM}^2}_{T_{CM}}+\underbrace{\frac{1}{2}\frac{m_1\cdot m_2}{M}|\dot{\vec{r}}|^2}_{T_{rel}} \end{align*}\]Al no tener en nuestro sistema fuerzas externas $\vec F_{ext}=0$ el centro de masas hará un movimiento rectilíneo uniforme $\begin{cases} v_{CM}=0& \\ v_{CM}=cte \end{cases}$.
Una vez fijada $v_{CM}$ a partir de las condiciones iniciales, será constante. Por tanto $T_{CM}$ es una constante en la energía de la cual podemos prescindir sin alterar la física del problema.
En los átomos hidrogenoides se cumple que $m_2\gg m_1$:
\[\begin{equation*} \vec{r}_{CM}=\frac{m_1\vec{r}_1+m_2\vec{r}_2}{m_1+m_2}=\cancelto{0}{\frac{m_1\vec{r}_1}{m_1+m_2}}+\frac{m_2\vec{r}_2}{m_1+m_2}\approx\vec{r}_2 \end{equation*}\]Usando esta propiedad y colocando el sistema de referencia en el centro de masas, queda que $|\vec{r}|=|\vec{r}_1|$ no es más que la distancia que separa ambas masas.
Definiendo $\mu\equiv\frac{m_1m_2}{M}$ la energía cinética con la que trabajaremos es:
La $E_{potencial}$ viene dada por la energía potencial de Coulomb debida a la interacción de una partícula con carga positiva $Ze$, donde $Z$ es el número de protones en el núcleo, y el electrón con carga negativa $-e$, suponiendo $4\pi\varepsilon_0=1$:
\[\begin{equation*} E_{potencial}\equiv U=-\frac{Ze^2}{r} \end{equation*}\]Finalmente, el Hamiltoniano del sistema es:
\[\begin{equation*} H=T+U=\frac{p^2}{2\mu}-\frac{Ze^2}{r} \end{equation*}\]Mecánica cuántica
En el paso a la mecánica cuántica:
\[\begin{equation} \hat{H}=\frac{\hat{p}^2}{2\mu}-\frac{Ze^2}{r}=-\frac{\hbar^2}{2\mu}\vec{\nabla}^2-\frac{Ze^2}{r}, \label{eq:ham} \end{equation}\]donde $\nabla^2$ es el operador laplaciano (a partir de aquí se usará la notación sin flecha) que debemos calcular para nuestras coordenadas.
Para el estudio de este sistema usamos la ecuación de Schrödinger independiente del tiempo ya que el Hamiltoniano no depende explícitamente de este:
\[\begin{equation*} \hat{H}\left|\Psi\right> =E\left|\Psi\right> \end{equation*}\]Usando \eqref{eq:ham} aquí, obtenemos la ecuación objeto de nuestro estudio:
\[\begin{equation*} \left[-\frac{\hbar^2}{2\mu}\nabla^2-\frac{Ze^2}{r}\right]\Psi=E\Psi, \end{equation*}\]donde $\Psi=\Psi (\xi,\eta,\phi)$.
Laplaciano en parabólicas
En orden a obtener la expresión del laplaciano en las coordenadas descritas en el enunciado del ejercicio, obtendremos primero una expresión general en coordenadas curvilíneas ortogonales $(u_1,u_2,u_3)$ de este.
Tenemos que relacionar las coordenadas cartesianas con estas:
El vector posición para un punto cualquiera es:
\[\begin{equation*} \vec{r}=x\hat{i}+y\hat{j}+z\hat{k} \end{equation*}\]donde $\hat{i}, \hat{j}, \hat{k}$ son los vectores unitarios en cartesianas.
El quid de la cuestión es obtener una representación de los vectores posición en términos de los vectores unitarios tangenciales (contravariantes) y normales (covariantes) de la base $(u_1,u_2,u_3)$.
Un vector tangente a la superficie dada por $u_1=c_1$ en un punto cualquiera es simplemente:
\[\begin{equation*} \frac{\partial r}{\partial u_1} \end{equation*}\]y un vector unitario en esa dirección:
\[\begin{equation*} e_1=\frac{\frac{\partial r}{\partial u_1}}{\norm{\frac{\partial r}{\partial u_1}}} \end{equation*}\]Definiendo el factor de escala $h_i\equiv\norm{\frac{\partial r}{\partial u_i}}$ podemos escribir:
\[\begin{equation*} \frac{\partial r}{\partial u_1}=h_1e_1 \end{equation*}\]Repitiendo esto para cada componente $i=1, 2, 3$:
\[\begin{equation} \frac{\partial r}{\partial u_i}=h_ie_i \label{eq:pdv} \end{equation}\]Un vector normal a la superficie dada por $u_1=c_1$ en un punto cualquiera es simplemente:
\[\begin{equation*} \nabla u_1 \end{equation*}\]Como antes los vectores unitarios para $i=1, 2, 3$:
\[\begin{equation*} E_1=\frac{\nabla u_1}{\norm{\nabla u_1}} \end{equation*}\]Queremos una expresión para $\nabla ^2=\nabla \cdot \nabla$. Comenzamos con el gradiente $\nabla\Phi$ que será de la forma:
\[\begin{equation*} \nabla\Phi=\sum_{i=1}^{3}f_ie_i \end{equation*}\]El elemento de línea:
\[\begin{equation*} d\vec{r}=\sum_{i=1}^{3}\frac{\partial r}{\partial u_i}du_i=\sum_{i=1}^{3}h_ie_idu_i \end{equation*}\]Donde hemos usado \eqref{eq:pdv}.
Entonces la derivada direccional para $\Phi$ es:
\[\begin{equation*} d\Phi=\nabla\Phi\cdot d\vec{r}=\sum_{i=1}^{3}\frac{\partial \Phi}{\partial u_i}du_i=\sum_{i=1}^{3}h_if_idu_i \end{equation*}\]Igualando coeficientes de los dos últimos términos obtenemos:
\[\begin{equation*} f_i=\frac{1}{h_i}\frac{\partial \Phi}{\partial u_i} \end{equation*}\]Luego el buscado gradiente en forma de operador:
\[\begin{equation*} \boxed{\nabla=\sum_{i=1}^{3}\frac{e_i}{h_i}\frac{\partial}{\partial u_i}} \end{equation*}\]Para seguir con la divergencia primero tenemos que indicar un par de condiciones:
- Los vectores $e_i$ para $i=1, 2, 3$ se comportan de manera cíclica al igual que los cartesianos.
- Haciendo el gradiente a $u_i$ obtenemos $\nabla u_i=\frac{e_i}{h_i}\implies \norm{\nabla u_i}=\frac{\norm{e_i}}{h_i}=\frac{1}{h_i}$
De estas condiciones obtenemos:
\[\begin{equation*} \nabla u_2 \times \nabla u_3 =\frac{e_2\times e_3}{h_2h_3}=\frac{e_1}{h_2h_3}\implies e_1=h_2h_3\nabla u_2 \times \nabla u_3 \end{equation*}\]De igual manera para $e_2$ y $e_3$.
Buscamos una expresión para $\nabla\cdot A$ donde $A=(A_1e_1,\ A_2e_2,\ A_3e_3)$; lo haremos para una componente y extrapolaremos el resultado para las otras dos.
\[\begin{equation*} \nabla\cdot(A_1e_1)=\nabla\cdot(A_1h_2h_3\nabla u_2 \times \nabla u_3) \end{equation*}\]Para continuar necesitamos usar el siguiente resultado matemático. Para un vector $B$ y una función diferenciable escalar $\Phi$:
\[\begin{equation*} \boxed{\nabla\cdot(\Phi B)=(\nabla \Phi)\cdot B+\Phi(\nabla\cdot B)} \end{equation*}\]Aplicando a nuestro caso $B=\nabla u_2 \times \nabla u_3$ y $\Phi=A_1h_2h_3$, tenemos:
\[\begin{align*} \nabla\cdot(A_1e_1)&=\nabla\cdot(A_1h_2h_3\nabla u_2 \times \nabla u_3)\:=\\ &=\nabla(A_1h_2h_3)\cdot \nabla u_2 \times \nabla u_3+A_1h_2h_3\underbrace{\nabla\cdot(\nabla u_2 \times \nabla u_3)}_{=\ 0}\:=\\ &=\nabla(A_1h_2h_3)\cdot\frac{e_2}{h_2}\times\frac{e_3}{h_3}=\nabla(A_1h_2h_3)\cdot\frac{e_1}{h_2h_3}\:=\\ &=\frac{e_1}{h_2h_3}\cdot\sum_{i=1}^{3}\frac{e_i}{h_i}\frac{\partial (A_1h_2h_3)}{\partial u_i}=\frac{1}{h_1h_2h_3}\frac{\partial}{\partial u_i}(A_1h_2h_3) \end{align*}\]Procediendo de forma análoga para las otras dos componentes de $A$ y agrupando:
\[\begin{equation*} \nabla\cdot A=\nabla\cdot (A_1e_1+A_2e_2+A_3e_3) \end{equation*}\] \[\begin{equation*} \boxed{\nabla\cdot A=\frac{1}{h_1h_2h_3}\left[\frac{\partial}{\partial u_1}(A_1h_2h_3)+\frac{\partial}{\partial u_2}(A_2h_1h_3)+\frac{\partial}{\partial u_3}(A_3h_1h_2)\right]} \end{equation*}\]Por fin estamos en posición de obtener el laplaciano $\nabla^2$ sin más que hacer $A=\nabla\Phi$ y entonces $A_i=\frac{1}{h_i}\frac{\partial \Phi}{\partial u_i}$:
\[\begin{equation*} \boxed{\Delta \Phi=\nabla\cdot \nabla\Phi=\nabla^2 \Phi=\frac{1}{h_1h_2h_3}\left[\frac{\partial}{\partial u_1}\left(\frac{h_2h_3}{h_1}\frac{\partial \Phi}{\partial u_1}\right)+\frac{\partial}{\partial u_2}\left(\frac{h_1h_3}{h_2}\frac{\partial \Phi}{\partial u_2}\right)+\frac{\partial}{\partial u_3}\left(\frac{h_1h_2}{h_3}\frac{\partial \Phi}{\partial u_3}\right)\right]} \end{equation*}\]Obteniendo las ecuaciones buscadas
Utilizando nuestras coordenadas:
\[\begin{alignat*}{2} & \begin{cases} x=\sqrt{\xi\eta}\cos(\phi),& 0\leq \xi\\ y=\sqrt{\xi\eta}\sin(\phi),& \eta < \infty \ ;\\ z=\frac{1}{2}(\xi - \eta) \end{cases} && \begin{cases} \xi=r+z,& \\ \eta=r-z,& \\ \phi=\arctan(\frac{y}{x}), \end{cases} \end{alignat*}\]El vector posición es:
\[\begin{align*} \vec{r}&=x\hat{i}+y\hat{j}+z\hat{k}\:=\\ &=\left(\sqrt{\xi\eta}\cos(\phi),\:\sqrt{\xi\eta}\sin(\phi),\:\frac{1}{2}(\xi - \eta)\right) \end{align*}\]Las derivadas parciales de primer orden de $(x,\ y,\ z)$ respecto de $(\xi,\ \eta,\ \phi)$:
\[\begin{alignat*}{3} &\frac{\partial x}{\partial \xi}=\frac{1}{2}\cos\phi(\xi\eta)^{-\frac{1}{2}}\eta\qquad&&\frac{\partial y}{\partial \xi}=\frac{1}{2}\sin\phi(\xi\eta)^{-\frac{1}{2}}\eta\qquad&&\frac{\partial z}{\partial \xi}=\frac{1}{2}\\ &\frac{\partial x}{\partial \eta}=\frac{1}{2}\cos\phi(\xi\eta)^{-\frac{1}{2}}\xi\qquad&&\frac{\partial y}{\partial \eta}=\frac{1}{2}\sin\phi(\xi\eta)^{-\frac{1}{2}}\xi\qquad&&\frac{\partial z}{\partial \eta}=-\frac{1}{2}\\ &\frac{\partial x}{\partial \phi}=-(\xi\eta)^{\frac{1}{2}}\sin\phi\qquad&&\frac{\partial y}{\partial \phi}=(\xi\eta)^{\frac{1}{2}}\cos\phi\qquad&&\frac{\partial z}{\partial \phi}=0 \end{alignat*}\]Los factores de escala correspondientes:
\[\begin{align*} h_{\xi}&=\norm{\frac{\partial \vec r}{\partial \xi}}=\sqrt{\left(\frac{\partial x}{\partial \xi}\right)^2+\left(\frac{\partial y}{\partial \xi}\right)^2+\left(\frac{\partial z}{\partial \xi}\right)^2}=\sqrt{\frac{1}{4}\frac{\xi+\eta}{\xi}}\\ h_{\eta}&=\norm{\frac{\partial \vec r}{\partial \eta}}=\sqrt{\left(\frac{\partial x}{\partial \eta}\right)^2+\left(\frac{\partial y}{\partial \eta}\right)^2+\left(\frac{\partial z}{\partial \eta}\right)^2}=\sqrt{\frac{1}{4}\frac{\xi+\eta}{\eta}}\\ h_{\phi}&=\norm{\frac{\partial \vec r}{\partial \phi}}=\sqrt{\left(\frac{\partial x}{\partial \phi}\right)^2+\left(\frac{\partial y}{\partial \phi}\right)^2+\left(\frac{\partial z}{\partial \phi}\right)^2}=\sqrt{\xi\eta} \end{align*}\]Expresando el operador laplaciano en coordenadas parabólicas:
\[\begin{align*} \Delta&=\frac{1}{h_\xi h_\eta h_\phi}\left[\frac{\partial}{\partial \xi}\left(\frac{h_\eta h_\phi}{h_\xi}\frac{\partial}{\partial \xi}\right)+\frac{\partial}{\partial \eta}\left(\frac{h_\xi h_\phi}{h_\eta}\frac{\partial}{\partial \eta}\right)+\frac{\partial}{\partial \phi}\left(\frac{h_\xi h_\eta}{h_\phi}\frac{\partial}{\partial \phi}\right)\right]\:=\\ &=\frac{4}{\xi+\eta}\left[\frac{\partial}{\partial \xi}\left(\xi\frac{\partial}{\partial \xi}\right)+\frac{\partial}{\partial \eta}\left(\eta\frac{\partial}{\partial \eta}\right)+\frac{\partial}{\partial \phi}\left(\frac{\xi+\eta}{4\xi\eta}\frac{\partial}{\partial \phi}\right)\right]\:=\\ &=\frac{4}{\xi+\eta}\left[\frac{\partial}{\partial \xi}\left(\xi\frac{\partial}{\partial \xi}\right)+\frac{\partial}{\partial \eta}\left(\eta\frac{\partial}{\partial \eta}\right)\right]+\frac{1}{\xi\eta}\frac{\partial^2}{\partial \phi} \end{align*}\]Ya podemos estudiar la ecuación de nuestro problema:
\[\begin{equation} \left[-\frac{\hbar^2}{2\mu}\nabla^2-\frac{Ze^2}{r}\right]\Psi=E\Psi \label{eq:resolver} \end{equation}\]Debemos tener en cuenta las siguientes relaciones:
\[\begin{equation*} \begin{cases} \lambda^2=-\frac{2\mu E}{\hbar^2}\implies E=-\frac{\lambda^2\hbar^2}{2\mu}& \\ r=\sqrt{x^2+y^2+z^2}=\frac{1}{2}(\eta+\xi) \end{cases} \end{equation*}\]Sustituyendo en \eqref{eq:resolver}:
\[\begin{equation*} \left[-\frac{\hbar^2}{2\mu}\nabla^2-\frac{2Ze^2}{\xi+\eta}\right]\Psi=-\frac{\lambda^2\hbar^2}{2\mu}\Psi \end{equation*}\]Multiplicamos por $-\frac{2\mu}{\hbar^2}$ a ambos lados:
\[\begin{equation} \left[\nabla^2+\frac{4\mu Ze^2}{(\xi+\eta)\hbar^2}\right]\Psi=\lambda^2\Psi \label{eq:ambos} \end{equation}\]Definimos la relación:
\[\begin{equation} \nu_1+\nu_2=-\frac{\mu Ze^2}{\hbar^2} \label{eq:cons} \end{equation}\]Introducimos \eqref{eq:cons} en \eqref{eq:ambos}:
\[\begin{equation*} \left[\nabla^2-\frac{4(\nu_1+\nu_2)}{\xi+\eta}\right]\Psi=\lambda^2\Psi \end{equation*}\]En este punto introducimos el operador laplaciano:
\[\begin{equation} \left\{\frac{4}{\xi+\eta}\left[\frac{\partial}{\partial \xi}\left(\xi\frac{\partial}{\partial \xi}\right)+\frac{\partial}{\partial \eta}\left(\eta\frac{\partial}{\partial \eta}\right)\right]+\frac{1}{\xi\eta}\frac{\partial^2}{\partial \phi^2}-\frac{4(\nu_1+\nu_2)}{\xi+\eta}\right\}\Psi=\lambda^2\Psi \label{eq:tocho} \end{equation}\]Si consideramos autofunciones de la forma:
\[\begin{equation*} \Psi (\xi,\eta,\phi)=f_1(\xi)f_2(\eta)e^{im\phi},\; m=0,\ \pm1,\ \pm2,\ \pm3... \end{equation*}\]Tenemos que:
\[\begin{align*} \frac{\partial \Psi}{\partial \phi}&=imf_1(\xi)f_2(\eta)e^{im\phi}\\ \frac{\partial^2 \Psi}{\partial \phi^2}&=-m^2f_1(\xi)f_2(\eta)e^{im\phi} \end{align*}\]Sustituimos en \eqref{eq:tocho}:
\[\begin{align*} &\frac{4}{\xi+\eta}\left[\frac{\partial}{\partial \xi}\left(\xi\frac{\partial}{\partial \xi}\right)+\frac{\partial}{\partial \eta}\left(\eta\frac{\partial}{\partial \eta}\right)\right]f_1(\xi)f_2(\eta)e^{im\phi}-\frac{m^2}{\xi\eta}f_1(\xi)f_2(\eta)e^{im\phi}\:-\\ &-\frac{4(\nu_1+\nu_2)}{\xi+\eta}f_1(\xi)f_2(\eta)e^{im\phi}=\lambda^2 f_1(\xi)f_2(\eta)e^{im\phi} \end{align*}\]Sacamos factor común $f_1(\xi)f_2(\eta)e^{im\phi}$ pasando todo a un lado y multiplicamos por $\frac{\xi+\eta}{4}$:
\[\begin{equation*} \boxed{\Bigg\{\left[\frac{\partial}{\partial \xi}\left(\xi\frac{\partial}{\partial \xi}\right)+\frac{\partial}{\partial \eta}\left(\eta\frac{\partial}{\partial \eta}\right)\right]-\frac{m^2}{4\xi\eta}(\xi+\eta)-(\nu_1+\nu_2)-\frac{\lambda^2 (\xi+\eta)}{4}\Bigg\}f_1(\xi)f_2(\eta)e^{im\phi}=0} \end{equation*}\]Esta es la ecuación de Schrödinger para un átomo hidrogenoide en coordenadas parabólicas.
Se debe cumplir para cualquier valor de $\xi,\ \eta,\ \phi$ por lo que podemos escribir dos ecuaciones separadas, una para $\xi$ y otra para $\eta$:
\[\begin{align*} &\left[\frac{\partial}{\partial \xi}\left(\xi\frac{\partial}{\partial \xi}\right)-\left(\frac{m^2}{4\xi}+\frac{\lambda^2}{4}\xi+\nu_1\right)\right]f_1(\xi)=0\\ &\left[\frac{\partial}{\partial \eta}\left(\eta\frac{\partial}{\partial \eta}\right)-\left(\frac{m^2}{4\eta}+\frac{\lambda^2}{4}\eta+\nu_2\right)\right]f_2(\eta)=0 \end{align*}\]Os dejo una versión PDF en este enlace.
Con esto concluye el primer artículo del blog. Espero que os haya gustado, ¡nos vemos en el siguiente!
